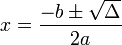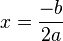|
نغمه ی عاشقی | ||
|
همانند حل معادلات درجه? اوّل برای پیدا کردن نقاط تقاطع معادله با محور
سپس با حل معادلهی فوق مقادیر
اگر ضرب چند عبارت برابر صفر شود، به این معنی است که حداقل یکی از عبارتها صفر است، و از آنجا که ما
برای حل معادله آن را تبدیل به مربع کامل میکنیم:
حالا از طرفین معادله جذر میگیریم تا مقدار
در نتیجه معادله دارای دو ریشه? زیر میباشد:
معمولاً عبارت طبق قضیه? تثلیث دلتا میتواند مقادیر زیر را اختیار کند:
حالتهای خاص و نکات معادلات درجه? دومدر معادله? کلی 1) اگر
و چون
و در ادامه:
2) اگر حاصلجمع اثبات (شرط:
طبق فرض :
از نظر جبری ریشهی مضاعف ریشهای است که زوج بار عبارت را صفر کند و ریشهی ساده ریشهای است که فرد بار یک عبارت را صفر کند ((البته در معادلاتی نظیر
3) اثبات (شرط : 4) اگر دلتای اثبات ( شرط :
نکته: همانطور که می دانید در صورتی که معادله دارای یک ریشه باشد یعنی تنها یک نقطه? تماس با محور xها دارد، در این صورت آن نقطه تنها میتواند نقطه? مینیمم یا ماکسیمم باشد، پس داریم :
با گرفتن مشتق داریم:
همچنین جالب است بدانید مجموع دو ریشه در معادله? درجه دوم [ یکشنبه 92/11/6 ] [ 11:21 عصر ] [ دانشجوی ریاضی ]
[ نظرات () ]
|
||
| [ فالب وبلاگ : وبلاگ اسکین ] [ Weblog Themes By : weblog skin ] | ||
 ها صورت کلی
ها صورت کلی  را برابر صفر قرار میدهیم، پس داریم:
را برابر صفر قرار میدهیم، پس داریم:
 نمیتواند برابر با صفر باشد زیرا در این صورت
نمیتواند برابر با صفر باشد زیرا در این صورت  معادله را حل میکنیم:
معادله را حل میکنیم:

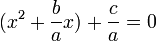
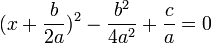
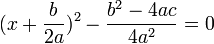

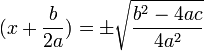

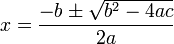
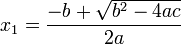
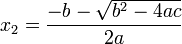
 را برابر با حرف دِلتای بزرگ
را برابر با حرف دِلتای بزرگ  نمایش میدهند، دِلتا در ریاضیات نماد فاصله یا تغییرات است.
نمایش میدهند، دِلتا در ریاضیات نماد فاصله یا تغییرات است.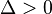 که در آن صورت فاصله? بین دو ریشه مثبت است، پس
که در آن صورت فاصله? بین دو ریشه مثبت است، پس 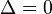 که در آن صورت فاصله? بین دو ریشه صفر است، پس هر دو جواب معادله یکی هستند و
که در آن صورت فاصله? بین دو ریشه صفر است، پس هر دو جواب معادله یکی هستند و 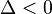 که در آن صورت فاصله? بین دو ریشه عددی منفی است و همانطور که میدانید فاصله نمیتواند
که در آن صورت فاصله? بین دو ریشه عددی منفی است و همانطور که میدانید فاصله نمیتواند باشد، یک ریشه صفر
باشد، یک ریشه صفر  و دیگری برابر با
و دیگری برابر با  است.
است.
 مینویسیم:
مینویسیم: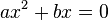
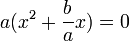


 برابر صفر شود، یعنی
برابر صفر شود، یعنی  در این صورت یکی از ریشهها
در این صورت یکی از ریشهها 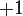 و دیگری
و دیگری  خواهد بود.
خواهد بود.

 همین تعریف کافی است ولی در دو طرف ریشه ساده علامت تابع فرق میکند ولی در دو طرف ریشه مضاعف علامت تابع یکسان است از نظر هندسی اگر بر محور طول ها طوری مماس شود که دو طرف نقطه در یک طرف محور طول ها بیفتد ریشه مضاعف داریم این نکته را فراموش نکنید که اگر ریشه معادلات درجه دو مضاعف باشد آن معادله مربع کامل است.
همین تعریف کافی است ولی در دو طرف ریشه ساده علامت تابع فرق میکند ولی در دو طرف ریشه مضاعف علامت تابع یکسان است از نظر هندسی اگر بر محور طول ها طوری مماس شود که دو طرف نقطه در یک طرف محور طول ها بیفتد ریشه مضاعف داریم این نکته را فراموش نکنید که اگر ریشه معادلات درجه دو مضاعف باشد آن معادله مربع کامل است.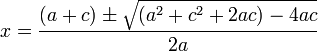

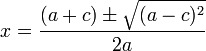
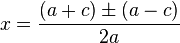


 : یک ریشه
: یک ریشه  و دیگری
و دیگری  خواهد بود
خواهد بود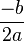 خواهد بود. (ریشهی مضاعف خواهد داشت، یعنی هردو
خواهد بود. (ریشهی مضاعف خواهد داشت، یعنی هردو